Abstract
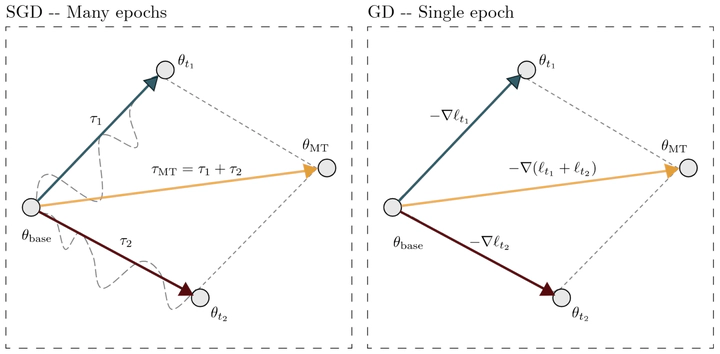
Task arithmetic has emerged as a simple yet powerful technique for model merging, enabling the combination of multiple finetuned models into one. Despite its empirical success, a clear theoretical explanation of why and when it works is lacking. This paper provides a rigorous theoretical foundation for task arithmetic by establishing a connection between task vectors and gradients of the task losses. We show that under standard gradient descent, a task vector generated from one epoch of finetuning is exactly equivalent to the negative gradient of the loss, scaled by the learning rate. For the practical multi-epoch setting, we prove that this equivalence holds approximately, with a second-order error term that we explicitly bound for feed-forward networks. Our empirical analysis across seven vision benchmarks corroborates our theory, demonstrating that the first-epoch gradient dominates the finetuning trajectory in both norm and direction. A key implication is that merging models finetuned for only a single epoch often yields performance comparable to merging fully converged models. These findings reframe task arithmetic as a form of approximate multitask learning, providing a clear rationale for its effectiveness and highlighting the critical role of early training dynamics in model merging.
Luca Zhou
Research Intern
Daniele Solombrino
PhD Student
🎓 Deep Learning PhD student @ 🎭 GLADIA (Sapienza) || 🔬 Research in 🧪 model merging, 🎶 audio gen, 🖌️ music edit.
Donato Crisostomi
PhD Student
PhD student @ Sapienza, University of Rome | former Applied Science intern @ Amazon Search, Luxembourg | former Research Science intern @ Amazon Alexa, Turin
